Cách Giải Cây Tìm Kiếm Nhị Phân (Binary Search Tree), Dể Hiểu

Bạn có bao giờ tự hỏi làm thế nào máy tính tìm kiếm thông tin một cách nhanh chóng không? Từ điển, danh bạ điện thoại, hay thậm chí các bài đăng trên mạng xã hội đều được tổ chức và tìm kiếm dựa trên những cấu trúc dữ liệu. Trong số đó, Cây Tìm Kiếm Nhị Phân là một trong những cấu trúc phổ biến nhất, ra đời từ nhu cầu tổ chức dữ liệu theo cách tối ưu hóa tốc độ tìm kiếm, thêm, và xóa.

Định Nghĩa

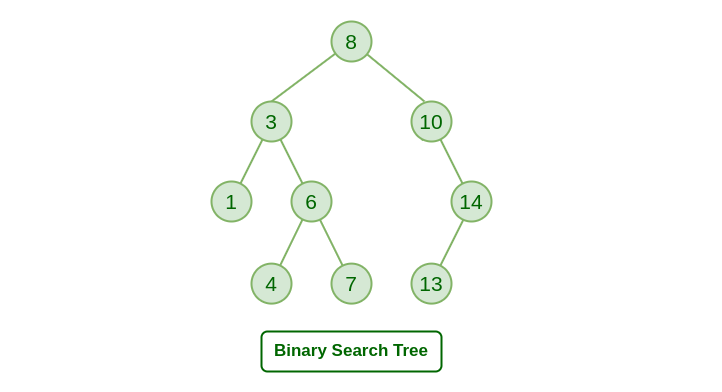
Cây Tìm Kiếm Nhị Phân (Binary Search Tree), hay viết tắt là BST, là một loại cây nhị phân đặc biệt. Bạn có thể tưởng tượng BST như một bản đồ nhỏ, nơi mỗi điểm giao nhau được gọi là “nút” và mỗi nút lưu trữ một giá trị.

Đặc điểm chính của BST là tính chất sắp xếp: giá trị của nút con bên trái luôn nhỏ hơn giá trị của nút cha, và giá trị của nút con bên phải luôn lớn hơn giá trị của nút cha. Tính chất này giúp BST có thể tìm kiếm dữ liệu rất nhanh, tương tự như cách bạn tìm từ trong từ điển.

Cây có thể phát triển từ một nút gốc duy nhất và mở rộng không giới hạn, miễn là nó duy trì nguyên tắc trên. Nếu một cây không tuân thủ quy tắc này, nó không được coi là một BST.

BST không chỉ là một cách tổ chức dữ liệu thông minh mà còn là nền tảng của nhiều thuật toán, từ sắp xếp đến xử lý dữ liệu.

Cách Giải

Cấu trúc dữ liệu Cây Tìm Kiếm Nhị Phân hoạt động trên nguyên tắc so sánh và sắp xếp. Sau đây là các phương thức quan trọng của nó:

• add: Thêm giá trị vào cây, duy trì quy tắc sắp xếp.
• findMin: Tìm giá trị nhỏ nhất trong cây.
• findMax: Tìm giá trị lớn nhất trong cây.
• isPresent: Kiểm tra xem một giá trị có tồn tại trong cây không.
• findMinHeight: Tìm chiều cao nhỏ nhất của cây.
• findMaxHeight: Tìm chiều cao lớn nhất của cây.
• isBalanced: Kiểm tra cây có cân bằng không.
• inOrder: Duyệt cây theo thứ tự tăng dần.
• preOrder: Duyệt cây bắt đầu từ nút gốc.
• postOrder: Duyệt cây kết thúc tại nút gốc.
• levelOrder: Duyệt cây theo tầng.
• reverseLevelOrder: Duyệt cây theo tầng ngược.
• remove: Xóa một giá trị khỏi cây.
• invert: Đảo ngược cây.
• isBinarySearchTree: Kiểm tra xem cây có phải BST không.

Bạn thấy đó, mỗi phương thức được thiết kế để tương tác với cây theo cách tối ưu và hiệu quả.

Triển Khai

Dưới đây là một cách triển khai Cây Tìm Kiếm Nhị Phân bằng TypeScript:

class Node {
  value: number;
  left: Node | null;
  right: Node | null;

  constructor(value: number) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  root: Node | null;

  constructor() {
    this.root = null;
  }

  // Thêm giá trị vào cây, duy trì quy tắc sắp xếp
  add(value: number) {
    const node = new Node(value);

    if (this.root === null) {
      this.root = node;
    }

    let current = this.root;

    while (current) {
      if (node.value === current.value) {
        return;
      }

      const dirrection = node.value < current.value ? 'left' : 'right';

      if (current[dirrection] === null) {
        current[dirrection] = node;
        return;
      }

      current = current[dirrection];
    }
  }

  // Tìm giá trị nhỏ nhất trong cây
  findMin(node = this.root) {
    if (node === null) {
      return null;
    }

    let current = node;

    while (current) {
      if (current.left === null) {
        return current.value;
      }

      current = current.left;
    }
  }

  // Tìm giá trị lớn nhất trong cây
  findMax(node = this.root) {
    if (node === null) {
      return null;
    }

    let current: Node | null = node;

    while (current) {
      if (current.right === null) {
        return current.value;
      }

      current = current.right;
    }
  }

  // Kiểm tra xem một giá trị có tồn tại trong cây không
  isPresent(value: number) {
    let current = this.root;

    while (current) {
      const dirrection = value < current.value ? 'left' : 'right';

      if (current.value === value) {
        return true;
      }

      current = current[dirrection];
    }

    return false;
  }

  // Tìm chiều cao nhỏ nhất của cây
  findMaxHeight() {
    const traverse = (node: Node | null): number => {
      if (node === null) return -1;

      return 1 + Math.max(traverse(node.left), traverse(node.right));
    };

    return traverse(this.root);
  }

  // Tìm chiều cao lớn nhất của cây
  findMinHeight() {
    const traverse = (node: Node | null): number => {
      if (node === null) {
        return -1;
      }

      return 1 + Math.min(traverse(node.left), traverse(node.right));
    };

    return traverse(this.root);
  }

  // Kiểm tra cây có cân bằng không
  isBalanced() {
    return this.findMinHeight() === this.findMaxHeight();
  }

  // Duyệt cây theo thứ tự tăng dần
  // https://www.youtube.com/watch?v=ne5oOmYdWGw
  inOrder = () => {
    if (this.root === null) return null;

    const traverse = (node: Node | null): number[] => {
      if (node === null) return [];

      const values: number[] = [];

      values.push(...traverse(node.left));
      values.push(node.value);
      values.push(...traverse(node.right));

      return values;
    };

    return traverse(this.root);
  };

  // Duyệt cây bắt đầu từ nút gốc
  // https://www.youtube.com/watch?v=gLx7Px7IEzg
  preOrder() {
    if (this.root === null) return null;

    const values: number[] = [];

    const traverse = (node: Node | null) => {
      if (node === null) return;

      values.push(node.value);
      traverse(node.left);
      traverse(node.right);
    };

    traverse(this.root);

    return values;
  }

  // Duyệt cây kết thúc tại nút gốc
  // https://www.youtube.com/watch?v=a8kmbuNm8Uo
  postOrder = () => {
    if (this.root === null) return null;

    const traverse = (node: Node | null): number[] => {
      if (node === null) return [];

      const values: number[] = [];

      values.push(...traverse(node.left));
      values.push(...traverse(node.right));
      values.push(node.value);

      return values;
    };

    return traverse(this.root);
  };

  // Duyệt cây theo tầng
  levelOrder = () => {
    if (this.root === null) return null;

    const results: number[] = [];
    const queue: Node[] = [this.root];

    const pushIfThere = (node: Node | null) => {
      if (node) queue.push(node);
    };

    while (queue.length) {
      const node = queue.shift()!;

      results.push(node.value);

      pushIfThere(node.left);
      pushIfThere(node.right);
    }

    return results;
  };

  // Duyệt cây theo tầng ngược
  reverseLevelOrder = () => {
    if (this.root === null) return null;

    const results: number[] = [];
    const queue: Node[] = [this.root];

    const pushIfThere = (node: Node | null) => {
      if (node) queue.push(node);
    };

    while (queue.length > 0) {
      const node = queue.shift()!;

      results.push(node.value);

      pushIfThere(node.right);
      pushIfThere(node.left);
    }

    return results;
  };

  // Xóa một giá trị khỏi cây
  remove = (value: number) => {
    const find = () => {
      if (this.root === null) return null;

      let parent: Node | null = null;
      let current = this.root;

      while (current) {
        if (current.value === value) {
          return { parent, current };
        }

        const dirrection = value < current.value ? 'left' : 'right';

        parent = current;
        current = current[dirrection]!;
      }

      return null;
    };

    const result = find();

    if (result === null) return null;

    const { parent, current } = result;

    const hasNoChildren = current.left === null && current.right === null;
    const hasOneChild = (current.left === null) !== (current.right === null);
    const hasTwoChilds = current.left && current.right;

    const dirrection = current === parent?.left ? 'left' : 'right';

    if (hasNoChildren) {
      if (current === this.root) {
        this.root = null;
      } else {
        parent![dirrection] = null;
      }

      return;
    }

    if (hasOneChild) {
      if (current === this.root) {
        this.root = this.root.left || this.root.right;
      } else {
        parent![dirrection] = current.left || current.right;
      }

      return;
    }

    if (hasTwoChilds) {
      const node = current === this.root ? this.root : current;

      const sucessorValue = this.findMin(node.right)!;

      this.remove(sucessorValue);

      node.value = sucessorValue;
    }
  };

  // Đảo ngược cây
  invert = () => {
    if (this.root === null) return null;

    const traverse = (node: Node | null) => {
      if (node === null) return;

      [node.left, node.right] = [node.right, node.left];

      traverse(node.left);
      traverse(node.right);
    };

    traverse(this.root);
  };

  // Kiểm tra xem cây có phải BST không
  static isBinarySearchTree(tree: BinarySearchTree) {
    const validate = (node: Node | null): boolean => {
      if (node === null) return true;

      if (node.left === null) {
        return true;
      } else if (node.left.value >= node.value) {
        return false;
      }

      if (node.right === null) {
        return true;
      } else if (node.right.value <= node.value) {
        return false;
      }

      return validate(node.left) && validate(node.right);
    };

    return validate(tree.root);
  }
}

Toàn Cảnh

Cây Tìm Kiếm Nhị Phân không chỉ là một cấu trúc độc lập mà còn là nền tảng cho nhiều cấu trúc khác như Cây AVL, Cây Đỏ-Đen, và Heap.

Nó giải quyết vấn đề tìm kiếm, không chỉ trong lập trình mà còn trong thực tế, như tổ chức thư viện sách hoặc quản lý dữ liệu khách hàng.

BST là một phần trong “bức tranh lớn” về thuật toán và cấu trúc dữ liệu. Mỗi phần trong bức tranh đó tương tác với BST để xử lý dữ liệu phức tạp hơn.

Hiểu BST là hiểu một mảnh ghép quan trọng trong hệ sinh thái công nghệ.

Ứng Dụng

Một ứng dụng thực tiễn của BST là trong các hệ thống cơ sở dữ liệu. Khi bạn tìm kiếm một khách hàng cụ thể trong hàng triệu dữ liệu, BST giảm đáng kể thời gian tìm kiếm.

BST còn được sử dụng để tạo ra bộ lọc email, tổ chức thư mục máy tính, hoặc thậm chí trong trò chơi điện tử để quản lý đối tượng trong thế giới ảo.

Trong lập trình, BST giúp tối ưu hóa thuật toán sắp xếp và tìm kiếm, hai bài toán thường xuyên xuất hiện.

Nhờ BST, chúng ta có thể tổ chức và truy cập dữ liệu nhanh chóng, chính xác.

Hiểu Lầm

Một hiểu lầm phổ biến là tất cả BST đều nhanh. Điều này không đúng nếu BST không được cân bằng, dẫn đến hiệu suất tìm kiếm giảm, tương tự như danh sách liên kết.

Một số người cũng nghĩ rằng BST là giải pháp tốt nhất cho mọi bài toán tìm kiếm. Tuy nhiên, trong một số trường hợp như dữ liệu không có thứ tự, Hash Table hiệu quả hơn.

BST cũng không phải lúc nào cũng dễ triển khai đúng cách, đặc biệt khi phải cân bằng cây hoặc xử lý dữ liệu động.

Hiểu nhầm này có thể khiến bạn áp dụng BST sai cách trong những bài toán không phù hợp.

Tóm Tắt

Cây Tìm Kiếm Nhị Phân là một cấu trúc dữ liệu mạnh mẽ, dựa trên nguyên tắc sắp xếp để tối ưu hóa tìm kiếm.

Nó không chỉ đơn giản mà còn là nền tảng của nhiều thuật toán và cấu trúc nâng cao.

Việc sử dụng BST đòi hỏi sự hiểu biết về lợi ích, hạn chế và ứng dụng phù hợp.

Hiểu BST là bạn đã bước thêm một bước vào thế giới của lập trình tối ưu hóa.

Nguồn: Viễn Đinh - Cách Giải Cây Tìm Kiếm Nhị Phân